Effective Ways to Calculate the Area of a Pyramid in 2025

Calculating the **area of a pyramid** is essential for various applications in mathematics, architecture, and education. As geometric properties of pyramids can be complex, understanding how to derive the **pyramid surface area** and **volume** is critical. This article provides expert tips and techniques for accurately calculating the area of different types of pyramids: square, rectangular, and triangular, amongst others. Whether you’re a student, teacher, or professional in the field of geometry and architecture, these insights will help enhance your understanding.

Understanding the Basic Properties of Pyramids

Pyramids are fascinating geometric shapes characterized by a polygonal base and triangular faces that converge at a single point called the **apex of a pyramid**. The base can vary in shape, giving rise to different types of pyramids, such as square, rectangular, and triangular. To calculate the **area of a pyramid**, one must first grasp its crucial measurements, which include **pyramid height**, **base area**, and **slant height**. This foundational knowledge is essential before diving into calculations, as it will inform how you use the **surface area formula** and the **formula for pyramid area**.

The Importance of Pyramid Dimensions

A pyramid’s dimensions directly impact its **volume measurement** and **surface area calculation**. For example, the **pyramid base area** is key in determining the overall size of the pyramid. To find the base area, apply specific geometric formulas based on the shape: use length squared for square pyramids or multiply length by width for rectangular bases. Meanwhile, the pyramid height, which is the perpendicular distance from the base to the apex, greatly influences the overall calculations. Remember that **calculating pyramid volume** also relies on these dimensions for accurate results.

Types of Pyramids and Their Calculations

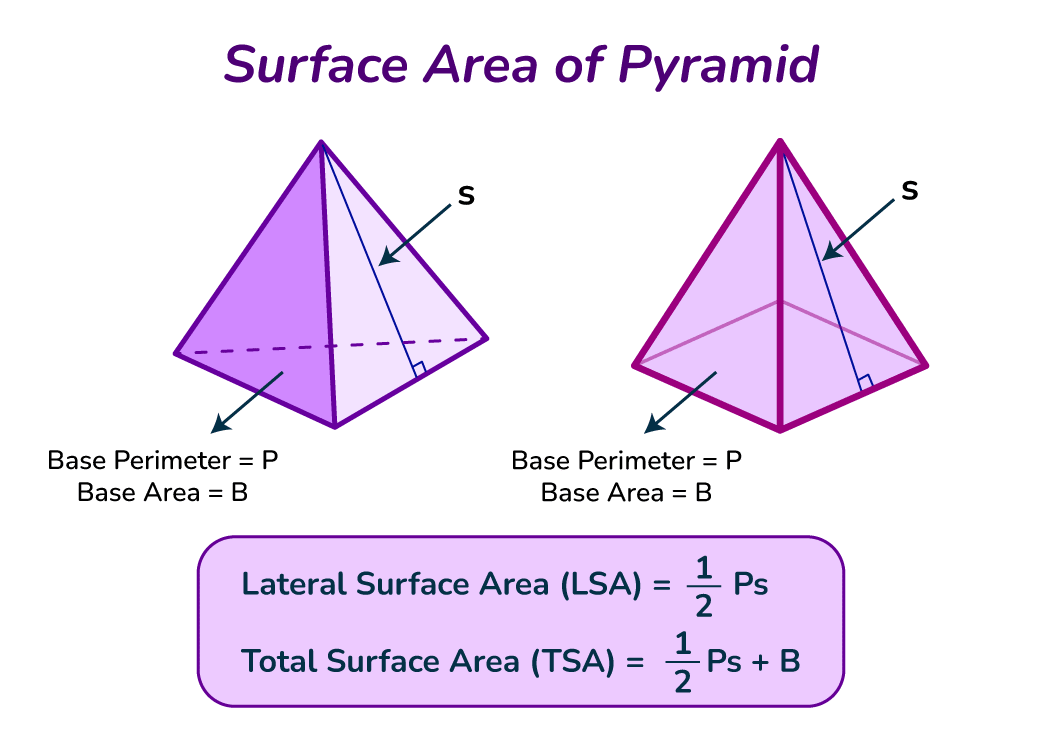
Different types of pyramids require tailored approaches when calculating their areas. **Square pyramids** possess a square base and have a straightforward area calculation procedure, while **triangular pyramids** entail calculating the area based on the specific triangular base shape. For each type of pyramid, there exists a specific **formula for surface area of a pyramid**, which typically combines the base area and the area of the lateral triangles. Understanding these distinctions simplifies the calculation process immensely.

Formulas for Calculating Area and Volume

Employing geometric formulas is fundamental when determining the **area** and **volume** of a pyramid. The most basic formula for calculating the area is to sum the base area and the lateral area—essentially the area of the triangular faces. The **formula for pyramid area** is expressed as \( A = B + L \), where \( A \) represents the total area, \( B \) is the **pyramid base area**, and \( L \) is the **pyramid lateral area**. For volume, the formula is \( V = \frac{1}{3} B \cdot h \), where \( V \) is volume, \( h \) is height, and \( B \) is the base area. Familiarizing oneself with these critical formulas facilitates efficient area calculations.

Step-By-Step Guide to Area Calculation

To effectively calculate the area of a pyramid, follow this step-by-step guide:

1. Identify the type of pyramid you are working with (e.g., square, rectangular, triangular).
2. Measure or obtain the **dimensions of the pyramid**, which include the base measurements and height.
3. Calculate the **base area** using the appropriate formula based on the base shape.
4. Determine the **lateral area** of each triangular face using the slant height and base edges.
5. Sum the base area and lateral area to find the total area of the pyramid.

Using this systematic approach can simplify the process and yield precise results in calculating both pyramid area and volume efficiently.

Utilizing CAD Software for Accuracy

With advancements in technology, tools like CAD software offer significant advantages for accurately calculating **pyramid measurements**. The use of such software can streamline complex calculations related to **geometric properties of pyramids**. By visualizing shapes, users can observe different configurations and derive metric calculations, reducing the risk of errors often associated with manual calculations. Whether for academic, construction, or architectural purposes, integrating CAD into calculations promotes accuracy and efficiency.

Applications and Real-Life Examples of Pyramids

Pyramids are more than academic concepts—they have practical applications in various fields. From architectural design with pyramids to their representation in nature, the versatility of these shapes is evident. For instance, the Great Pyramid of Giza is a notable example of pyramid geometry used in ancient architecture. By studying practical examples of **pyramid applications**, one can observe how **pyramid shapes** influence structures and designs. Moreover, in **teaching geometry with pyramids**, real-life examples not only engage students but also deepen their understanding of technical concepts through tangible illustrations.

Understanding Geometric Shapes in Nature

Pyramids also resonate in nature; from the formation of certain crystals to mountain shapes, the instinct of **geometric shapes** appears prominently. By examining **pyramid shapes in nature**, it becomes clear how these forms are integrated into biological structures and physical phenomena. Teachers can leverage these connections to enhance spatial awareness and practical geometry lessons that show how shapes interact within the environment.

Architectural Design with Pyramids

Architecturally, the use of pyramid structures can be seen in designs aiming to combine aesthetic beauty with functional performance. For example, pyramidal roofs are commonly found in various cultural designs for their strength against elements. Moreover, engaging with pyramids in architecture enables the exploration of geometry in creating sustainable designs, showcasing the **importance of pyramids** in the field. Understanding their properties promotes creative design solutions which are crucial in modern architecture.

Key Takeaways

• Understand the basic geometric properties and dimensions of pyramids for accurate calculations.
• Utilize well-defined formulas to calculate pyramid area and volume effectively.
• Leverage technology like CAD software for precise dimensional analyses.
• Recognize the significant real-life applications and importance of pyramids across various fields.
• Incorporate visual aids and nature examples in teaching to enrich learners’ understanding of geometric concepts.

FAQ

1. What is the formula for the surface area of a pyramid?

The surface area of a pyramid can be calculated using the formula \( A = B + L \), where \( A \) is the total surface area, \( B \) is the base area, and \( L \) represents the lateral area of the triangular faces. Depending on the type of pyramid, make sure to use the correct measurements for each calculation.

2. How do I calculate the volume of a triangular pyramid?

The volume of a triangular pyramid can be calculated using the formula \( V = \frac{1}{3} B \cdot h \), where \( B \) is the area of the triangular base and \( h \) is the height from the base to the apex. It’s critical to ensure that base area and height are measured using consistent units for accurate results.

3. Can CAD software help in calculating the area of pyramids?

Yes, CAD software can greatly assist in calculating the area and volume of pyramids. By providing visual representations and 3D models, users can define measurements accurately and visualize dimensions effectively, reducing human error substantially.

4. What types of pyramids exist?

There are several types of pyramids, including the **square pyramid**, **rectangular pyramid**, and **triangular pyramid**, each categorized by their base shape. Understanding these pyramid classifications is essential for accurately calculating their volume and surface area.

5. How are pyramids used in real-life applications?

Pyramids are utilized in various real-life scenarios, from architectural designs—like pyramid-shaped roofs—to their occurrence in nature, such as mountain structures and crystal formations. Recognizing these applications enriches the understanding of geometry beyond theoretical concepts.

By exploring and understanding the area of a pyramid, one can appreciate the vast implications this geometry has across multiple disciplines—from education and mathematical applications to architectural wonders. Start expanding your geometric knowledge today!